In the case of a lack of in-flow of a leaking tank, it is a mistake to think that it will be definitely end up emptying completely.
At first a lack
of in-flow leads to a drop in water level.
But, as this level drops, the pressure on the leak reduces and the out-flow
ends up equaling the in-flow.
The water level will, therefore, stabilize.
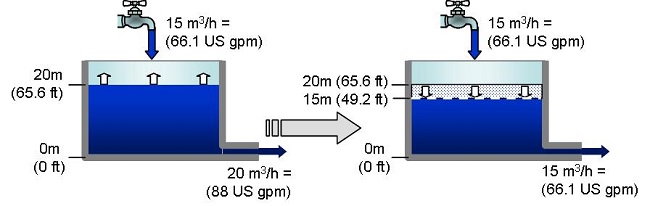
The in-flow is less than the out-flow, these flows end up being equal
In the case of a lack of heat output in a home, we don’t always end up
freezing!
The room being heated normally, a sudden lack of heat will lead to a drop in
ambient temperature.
But, as this temperature drops, the difference between interior and exterior
temperature diminishes, and so the heat losses reduce.
When these losses equal the heating output, the ambient temperature will
stabilize.
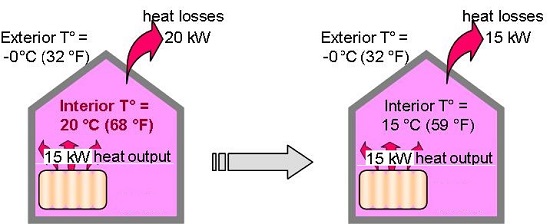
The heating output is less than the heat losses, these outputs end up being equal
Question
We arrive in an un-heated house in the country. The interior temperature is the same as the exterior.
This is stable at 0 [°C] (32°F).
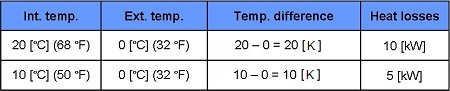
We know that the heat losses of the house at 20 [°C] (68°F) interior and 0 [°C] (32°F) exterior are of 10 [kW].
We switch on some independent electric radiators, of a total power of 5 [kW].
What interior temperature can we hope to obtain? Why?
We can hope to increase the interior temperature to 10 [°C] (50°F).
In fact, if the heat losses of the house at 20 [°C] (68°F) interior and 0 [°C] (32°F) exterior are of 10 [kW] (a difference of 20 [K]), at 10 [°C] (50°F) interior and 0 [°C] (32°F) exterior, the losses are of 5 [kW]).
The heat losses are in proportion to the difference between interior and exterior temperature:At 10 [°C] (50°F) interior and 0 [°C] (32°F) exterior, the output of the radiators (5 [kW]) will equal the heat losses (5 [kW]).
After the temperature increase phase, the interior temperature will remain stable.
Question
We have understood that in the house studied in the previous exercise, at 0 [°C] (32°F) interior and 0 [°C] (32°F) exterior, it is possible to raise interior temperature by 10 [K] with 5 [kW] of independent heating.
Why, when the output supplied by the radiators equals the heat losses at 10 [°C] (50°F) interior and at 0 [°C] (32°F) exterior, the increase in temperature will be slow and require several hours?
The period of temperature increase is subject to the thickness of the walls of the house.
In fact, the heat given out by the radiators is used both to warm up the room air temperature (requiring little heat) but also to warm up the temperature of the walls (requiring a lot of heat).
The duration of this temperature increase is subject to the inertia of the building.
Question
We arrive in the un-heated house in the country. The interior temperature is the same as the exterior.
This is stable at +10 [°C] (50 °F).
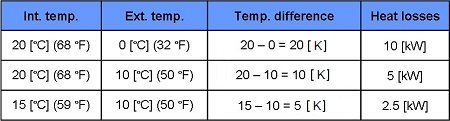
We know that the heat losses of the house at 20 [°C] (68 °F) interior and 0 [°C] (32 °F) exterior are of 10 [kW].
We switch on an independent electric radiator, of a total power of 2.5 [kW].
To what interior temperature can we hope to heat the house? Why?
We can hope to heat the house to a temperature of 15 [°C] (59°F).
We have understood in the previous exercises that the heat losses of the house are 10 [kW] (a difference of 20 [K], a heat output of half the heat loss (5 [kW]), permits a temperature increase of 10 [K].
With half as much heat output (2.5 [kW]), we can hope to increase temperature by only 5 [K].
The heat losses are in proportion to the difference between interior and exterior temperature :At 15 [°C] (59°F) interior and +10 [°C] (50°F) exterior, the output of the radiators (2.5 [kW]) will equal the heat losses (2.5 [kW]).
After the temperature increase phase, the interior temperature will remain stable.
Question
We can hope to heat the house to a temperature of 15 [°C] (59°F).
We have understood in the previous exercises that the heat losses of the house are 10 [kW] (a difference of 20 [K], a heat output of half the heat loss (5 [kW]), permits a temperature increase of 10 [K].
With half as much heat output (2.5 [kW]), we can hope to increase temperature by only 5 [K].
The heat losses are in proportion to the difference between interior and exterior temperature :
We can hope to heat the house to a temperature of 15 [°C] (59°F).
We have understood in the previous exercises that the heat losses of the house are 10 [kW] (a difference of 20 [K], a heat output of half the heat loss (5 [kW]), permits a temperature increase of 10 [K].
With half as much heat output (2.5 [kW]), we can hope to increase temperature by only 5 [K].
The heat losses are in proportion to the difference between interior and exterior temperature :At 15 [°C] (59°F) interior and +10 [°C] (50°F) exterior, the output of the radiators (2.5 [kW]) will equal the heat losses (2.5 [kW]).
After the temperature increase phase, the interior temperature will remain stable.