Q = M C ΔT formula was conceived to calculate quantities of sensible heat Q. But it can be manipulated to calculate heated masses or differences in temperature, once the other values are known:
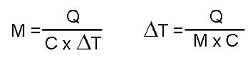
These are not new formulas; simply variations of the formula Q = M C ΔT, depending onwhat we know, and what we are looking for.
The units used must obviously be the same whatever the presentation of the formula, thus:
Q in [kJ]
M: mass in [kg]
C in [kJ/kg.K]
ΔT in [K]

Question
What mass of water in [kg] could be heated by 40 [K] if 162,000 [kJ] (153,546 Btu) were available?
968.9 [kg]
Explanation:
The specific heat of water is 4.18 [kJ/kg.K]
The mass of water that could be heated by de 40 [K], with 162,000 [kJ] will be:
162,000/(4.18 x 40) = 968.9 [kg]
Question
By how many degrees in [K] could we heat 3,000 [l] of water with a supply of 540,000 [kJ]?
43 [K]
Explanation:
The specific heat of water is 4.18 [kJ/kg.K] (3.96 Btu/kg.K)
The considered density of water is 1,000 [kg/m3].
Hence 3,000 [l] = 3,000 [kg]
With a supply of 540,000 [kJ] the rise in temperature of 3,000 [l] will be:
540,000/(3,000 x 4.18) = 43 [K]

Question
With the specific heat of air being 1 [kJ/kg.K], what mass of air (in [kg]) could we heat from 10 to 35 [°C] with a supply of 15,000 [kJ] (14,217 Btu)?
600 [kg]
Explanation:
500 [m3]
The mass of air heated from 10 to 35 [°C] with a supply of 15,000 [kJ] will be:
15,000/(1 x 25) = 600 [kg]
Hence the volume of air heated will be 600/1.2 = 500 [m3]
Question
The specific heat of domestic fuel is 2.1 [kJ/kg.K] (1.99 Btu/kg.K).
The density of domestic fuel is 840 [kg/m3].
What quantity of heat needs to be applied to a tank of 25 [m3] to heat it from 5 to 15 [°C]?
441,000 [kJ] (417,987 Btu)
Explanation:
The mass of domestic fuel that can be heated is: 25 x 840 = 21,000 [kg]
The quantity of heat to be applied to the tank to raise the temperature of the fuel by 10 [K] will be: 21,000 x 2.1 x 10 = 441,000 [kJ]
Question
The specific heat of domestic fuel is 2.1 [kJ/kg.K] (1.99 Btu/kg.K).
What mass of domestic fuel could be heated by 25 [K], with 864,000 [kJ] (818,913 Btu)?
Knowing that the density of domestic fuel is 840 [kg/m3], what volume of fuel (in [m3]) could be heated?
16 457 [kg]
19.59 [m3]Explanation:
The mass of domestic fuel to be heated will be: 864,000/(2.1 x 25) = 16,457 [kg]
The volume of fuel heated will be: 16,457/840 = 19.59 [m3]
Question
The specific heat of domestic fuel is 2.1 [kJ/kg.K] (1.99 Btu/ kg K).
The density of domestic fuel is 840 [kg/m3].
By how many degrees [°C] or ([K]) could we heat a tank of 6 [m3], with 72,000 [kJ] (68,242 Btu)?
6.8 [K]
Explanation:
The mass of domestic fuel to be heated will be:
6 x 840 = 5,040 [kg]
The rise in temperature of this mass of domestic fuel with 72,000 [kJ] available will be:
72,000/(5,040 x 2.1) = 6.8 [K]
Question
By how many degrees [K] could we heat 1 [kg] of water if 1,000 Joules (0.95 Btu) are supplied?
0.24 [K]
Explanation:
The specific heat of water is 4.18 [kJ/kg.K] (3.96 Btu/kg.K)
1,000 Joules corresponds to 1 [kJ]
The rise in temperature of 1 [kg] of water with a supply of 1 [kJ] will be:
1/4.18 = 0.24 [K]
